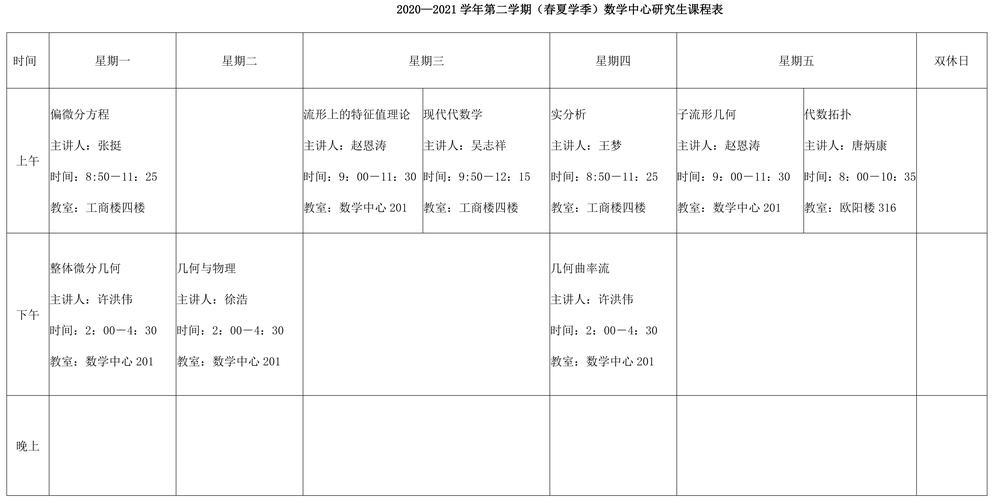
研究生數(shù)學(xué)課程
研究生數(shù)學(xué)課程通常涵蓋了更高級(jí)和更專業(yè)的數(shù)學(xué)領(lǐng)域,這些課程可能會(huì)因?qū)W校和專業(yè)方向的不同而有所差異。以下是一些常見的研究生數(shù)學(xué)課程:
1. 高級(jí)微積分:深入研究微積分的理論和應(yīng)用,包括多重積分、偏微分方程、變分法等。
2. 線性代數(shù):進(jìn)一步探討矩陣?yán)碚摗⑾蛄靠臻g、線性變換、特征值問題等。
3. 概率論與數(shù)理統(tǒng)計(jì):研究隨機(jī)事件的概率、隨機(jī)變量及其分布、大數(shù)定律、中心極限定理、統(tǒng)計(jì)推斷等。
4. 復(fù)分析:研究復(fù)數(shù)函數(shù)的性質(zhì),包括解析函數(shù)、復(fù)積分、留數(shù)定理等。
5. 實(shí)分析:研究實(shí)數(shù)函數(shù)的性質(zhì),包括勒貝格積分、測(cè)度論、函數(shù)空間等。
6. 拓?fù)鋵W(xué):研究空間的連續(xù)性和連通性,包括點(diǎn)集拓?fù)洹⒋鷶?shù)拓?fù)涞取?/p>
7. 抽象代數(shù):研究代數(shù)結(jié)構(gòu),如群、環(huán)、域等。
8. 偏微分方程:研究偏微分方程的解法和應(yīng)用,包括橢圓型、雙曲型和拋物型方程。
9. 數(shù)值分析:研究數(shù)值方法在解決數(shù)學(xué)問題中的應(yīng)用,如數(shù)值積分、數(shù)值微分、數(shù)值解方程等。
10. 優(yōu)化理論:研究如何找到問題的最優(yōu)解,包括線性規(guī)劃、非線性規(guī)劃、動(dòng)態(tài)規(guī)劃等。
11. 圖論與組合數(shù)學(xué):研究圖的結(jié)構(gòu)和性質(zhì),以及組合數(shù)學(xué)中的計(jì)數(shù)問題。
12. 數(shù)學(xué)建模:將數(shù)學(xué)理論應(yīng)用于實(shí)際問題,建立數(shù)學(xué)模型并進(jìn)行分析。
這些課程不僅為研究生提供了深入的數(shù)學(xué)知識(shí),還為他們?cè)诳蒲泻凸こ填I(lǐng)域中的應(yīng)用打下了堅(jiān)實(shí)的基礎(chǔ)。如果你有特定的課程或領(lǐng)域感興趣,可以進(jìn)一步探討。

 微信掃一掃打賞
微信掃一掃打賞